Qué es el problema de los tres cuerpos, la fórmula “imposible” que después de siglos aún desvela a la ciencia

La novela “El problema de los tres cuerpos” del escritor e ingeniero chino Liu Cixin se convirtió en bestseller al poco tiempo de ser publicada en 2006. Casi un par de décadas después, volvió a estar en boca de todos después de que Netflix estrenara la serie basada en el libro. Hoy también es uno de los títulos más elegidos en la plataforma.

Tanto en el libro como en la serie, los personajes interactúan con un planeta misterioso llamado Trisolaris. El planeta gira alrededor de tres soles al mismo tiempo. Por la inestabilidad de la órbita, las civilizaciones tienen eras de calma, pero también sufren de períodos de caos, de poblaciones enteras destruidas. Los científicos, entonces, buscan una solución a ese dilema que parece irresoluble.

En realidad, la premisa de la historia se basa en un problema real de la física. Un problema que data de cientos de años atrás, que incluso se remonta a épocas de Issac Newton, quien fue el primero en proponer el concepto de gravedad. Por sus leyes, los físicos saben que es posible determinar las posiciones y velocidades futuras de dos cuerpos, cualquiera sea su masa, que se someten a atracción gravitacional mutua. Un ejemplo concreto es un sistema solar formado tan solo por un sol y un planeta. Por su órbita predecible, se podría decir con total precisión dónde van a estar en cada momento.

El problema surge cuando son más de dos cuerpos los involucrados. El movimiento de tres o más cuerpos sometidos a gravedad mutua resulta imposible de predecir. Hace más de 120 años, el matemático francés Henri Poincaré mostró que no hay una solución general para el problema expresable en una fórmula. Los objetos pueden dibujar trayectorias irregulares, hasta colisionar entre ellos.

“Esto significa que, en general, sus órbitas no son estables ni predecibles. Podemos hacer algunas predicciones mediante simulaciones numéricas, pero son muy inestables y dependen del conocimiento exacto de las condiciones iniciales. Es necesario saber exactamente dónde está cada uno de los cuerpos, a qué velocidad y en qué dirección se mueven para poder predecir dónde estarán en un momento posterior. Si estas condiciones iniciales se equivocan aunque sea un poco, con el tiempo la predicción empeorará porque dará un resultado completamente diferente en el futuro. Estos se conocen como sistemas ‘caóticos’”, explicó Matthew Kenzie, profesor de Física en la Universidad de Cambridge, en diálogo con Infobae.

-Entonces, ¿tres cuerpos no pueden coexistir?

-Sí, tres cuerpos pueden coexistir (y sabemos de ellos en el universo), pero si están en órbitas caóticas, coexisten de manera estable durante un tiempo y eventualmente uno de los cuerpos es expulsado del sistema o dos de los cuerpos chocan.

-¿Cuál es la teoría que más se acerca a la solución?

-No hay ninguna. Existen algunas soluciones muy específicas, pero no existe una solución general. Es probable que en realidad no exista una solución analítica, aunque tal vez nuestras matemáticas no sean lo suficientemente avanzadas.

En la serie, los personajes interactúan con un misterioso planeta que gira alrededor de tres soles

El problema de los tres cuerpos no desafía las leyes de la física. Es simplemente una “característica” de ellas. Durante siglos -y aún hoy- científicos se abocan a su estudio porque el problema de los n cuerpos (tres o más) son muy habituales, tanto que convivimos con ellos, con el sistema solar o con la galaxia. El pronóstico del clima, por caso, es un ejemplo recurrente de cómo los meteorólogos se esfuerzan por modelar un sistema caótico.

Sarah Rugheimer, astrobióloga y profesora de la Universidad de York, dice que el dilema es solo “un artefacto de cómo interactúan gravitacionalmente múltiples cuerpos”. Al no haber una solución analítica, que resuelva el problema en general, se utilizan métodos numéricos para llegar a resultados que no son del todo concluyentes.

“En general, estos cálculos sólo se hacen numéricamente, por lo que, por ejemplo, no podemos conocer exactamente la formación del sistema solar miles de millones de años más adelante”, señaló la experta. “Nuestro sistema Tierra-Luna-Sol es un ejemplo de cómo se puede tener un problema restringido de tres cuerpos asumiendo que uno tiene un efecto insignificante. Eso hace que nuestras tres órbitas sean estables”.

Tierra-Luna-Sol

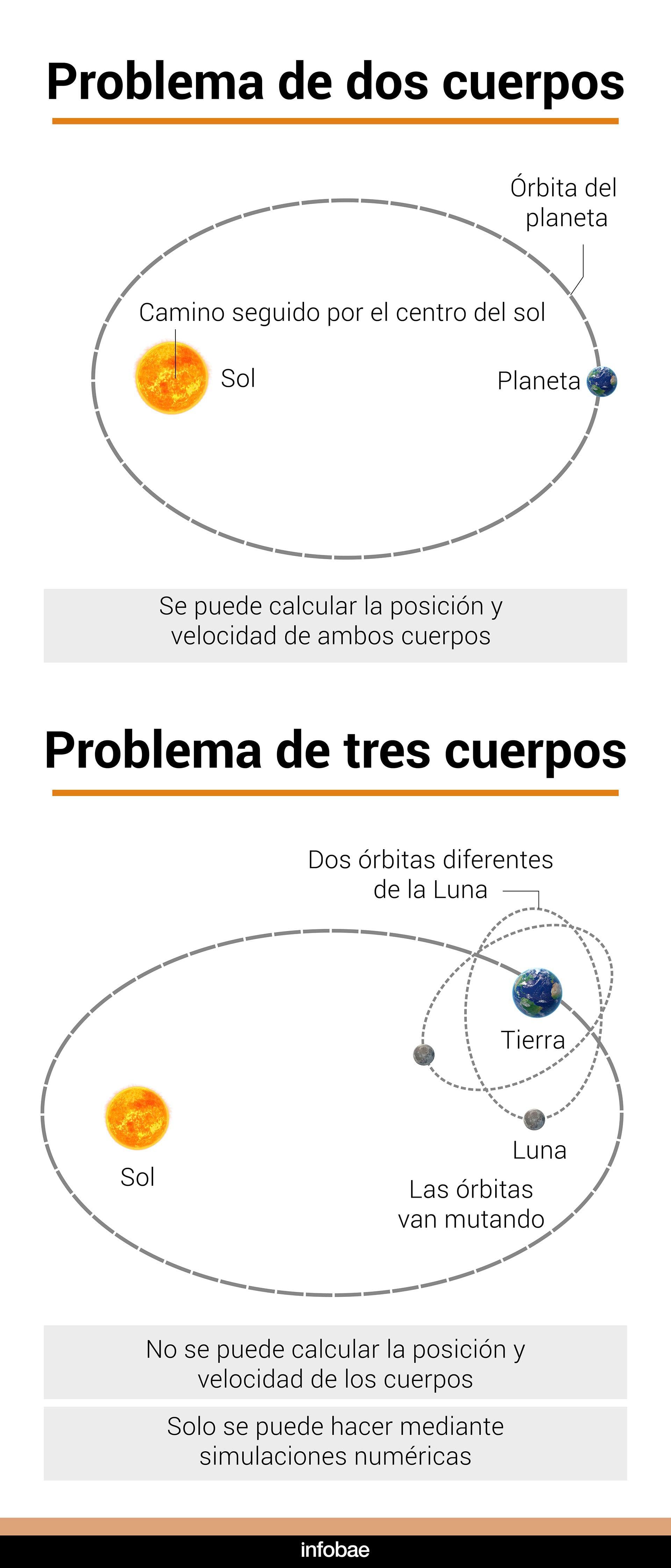
El problema de los tres cuerpos no es una elucubración teórica. Es un problema real. Hay sistemas formados por tres estrellas, o sistemas planetarios con un sol y dos planetas. Resulta imposible calcular con exactitud el movimiento de tres o más cuerpos que ejercen gravedad entre ellos porque el sistema es caótico.

“Una pequeña perturbación en las condiciones iniciales se transforma, al cabo de poco tiempo, en una enorme perturbación que afecta la estabilidad. Todo depende de las condiciones iniciales”, explicó a Infobae Gustavo Romero, profesor de Astrofísica en la Universidad Nacional de La Plata y director del Instituto Argentino de Radioastronomía.

Romero aclaró que, si bien los sistemas caóticos no son predecibles a largo plazo, son deterministas. Esto quiere decir que sus estados futuros dependen de sus estados pasados y de las leyes naturales. “Si el sistema además de determinista es caótico, lo que sucederá está determinado por lo que sucedió y por las leyes naturales, pero no es predecible a largo plazo por nuestras teorías. Un ejemplo es el tiempo meteorológico o el problema de muchos cuerpos”, advirtió.

Dentro de esos problemas, el más importante es el de Tierra-Luna-Sol, que forma un sistema muy parecido al de los tres cuerpos, más una pequeña perturbación que suman el resto de los planetas y asteroides. Lo que a la ciencia le importa es saber si ese trinomio es estable a largo plazo. Si no lo fuera, podría haber consecuencias devastadoras: la luna podría escapar y chocar contra la Tierra.

“El sistema Tierra-Luna-Sol es estable sobre escalas de cientos de millones de años, a menos que se introduzcan perturbaciones externas como el paso cercano de una estrella, un agujero negro o un asteroide grande. En el sistema solar completo, la estabilidad es menor y por eso cada tanto cometas y asteroides salen disparados en dirección al Sol, que es el objeto más masivo”, indicó el astrofísico.

Cuando se trata de solo dos cuerpos -sistemas binarios formados por dos estrellas o una estrella y un agujero negro- el problema se puede resolver matemáticamente. En cambio, cuando se agrega uno o más cuerpos, se realizan simulaciones numéricas, se juega con las variables para llegar a resultados a corto o mediano plazo. Las soluciones, aunque rebatibles, se multiplican.

Miles de soluciones (o ninguna solución)

El problema de los tres cuerpos hoy tiene miles de soluciones diferentes. Hasta hace una década, eran apenas un puñado de alternativas que los científicos, mediante simulaciones, habían propuesto. Pero el surgimiento de las supercomputadoras profundizó la exploración de ecuaciones y, en 2023, por ejemplo, ya se hablaba de más de 12 mil soluciones.

Alfonso Población Sáez es matemático. Enseña matemática aplicada en la Universidad de Valladolid. Consultado por Infobae, explica por qué no se puede llegar a una ecuación analítica, que responda al fondo de la cuestión. ¿Por qué, en su lugar, es necesario apelar a variables simuladas?

-Para conocer la posición y velocidad de un cuerpo cualquiera sometido a una fuerza necesitamos conocer seis parámetros: tres corresponden a sus coordenadas espaciales (x, y, z), y las otras tres a las velocidades respecto a las tres direcciones posibles (vx, vy, vz). En el caso de dos cuerpos sometidos a las fuerzas de atracción gravitacional de uno sobre el otro, tendríamos que determinar doce parámetros, y eso es posible porque las ecuaciones de sus movimientos pueden resolverse para cualquier conjunto de condiciones iniciales. Sin embargo, con tres cuerpos (en este caso habría que determinar 18 parámetros), esas mismas ecuaciones no nos dan una solución cerrada.

-Se necesita entonces aplicar otro método.

-Exacto. El procedimiento empleado para dos cuerpos no sirve para tres o más cuerpos. Lo único que puede hacerse es, con los grados de libertad que hay -la cantidad de parámetros sin poder resolverse-, dar por supuestos algunos valores y ver qué ocurre. O sea hacer simulaciones; algunas de las cuales nos llevan a comportamientos caóticos, aleatorios incluso. Es algo tan sencillo y elemental como eso, no hay que buscar explicaciones esotéricas.

Cuando se trata de tres cuerpos o más que ejercen gravedad mutua, los científicos apelan a ecuaciones simuladas

-¿Se puede decir que el problema es irresoluble?

-No se ha demostrado que el problema sea irresoluble, que no tenga solución. Por ejemplo, la cuadratura del círculo se sabe que es irresoluble, hay una demostración de que no se puede resolver. Pero para el problema de los tres cuerpos, mientras no se descubra una demostración que indique que el problema no tiene solución, la tiene. Aparecerán nuevas técnicas para intentar resolverlo o no. En cualquier caso, es lo que los matemáticos llamamos una cuestión abierta.

-¿Por qué cree que suscitó tanto interés a lo largo de los siglos en la ciencia y ahora también en la población general?

-Todos los problemas sin resolver -y en matemáticas hay muchos, y algunos con muchos siglos de antigüedad- suscitan interés en la comunidad científica y en la sociedad en general, más aún si tienen un enunciado sencillo y fácil de entender por cualquiera. A esto se le añade en este caso que, si echamos una mirada al espacio exterior, no son tres cuerpos precisamente los que se encuentran en una “perfecta” armonía, sino muchos. No poder resolver el caso con solamente tres y sin embargo comprobar que ahí fuera la situación es “estable”, es como para que pensemos: “Creemos que controlamos todo y en realidad no tenemos ni idea”.

-¿Qué opina que ahora el tema esté en boca de mucha gente ajena a la ciencia?

-En ciencia no hay nada “de moda”. Los enigmas están ahí desde que se plantean o aparecen. La moda la provoca una novela, una serie, una película difundida por medios de comunicación u otros agentes. En otros momentos estuvo “de moda” los viajes en el tiempo. Pero los científicos trabajan en estos asuntos independientemente de que esté de actualidad o no.

.¿Cree que aparecerá por fin la solución en algún momento?

-Hay problemas planteados de tiempos de los griegos, siglos antes de Cristo, y a día de hoy no se sabe si tienen solución o no la tienen. De modo que lo único que queda es seguir trabajando en ello, y tener paciencia. Esto es como encontrar un remedio contra enfermedades mortales, aunque menos dramático, claro. Para el ciudadano medio puede resultar frustrante, pero en ciencia las cosas funcionan así.